I made a video about a specific technique to solve this puzzle using fingerprinting a while ago.
This technique is more efficient and faster than most methods I have seen online, but I still wondered if better, faster or fancier ways were possible.
So instead of building an actually fancier program, I created this:
([a-g ]+) \| ([a-g]+) ([a-g]+) ([a-g]+) ([a-g]+)
$1 | $2 ¶ $1 | $3 ¶ $1 | $4 ¶ $1 | $5
%(`([a-g ]+) \| ([a-g]+)
K`$1¶R`[$2]¶_
~`$-
_
[^_]
(_+)
$.1
%)`
42
0
17
1
34
2
39
3
30
4
37
5
41
6
25
7
49
8
45
9
(\d)¶(\d)¶(\d)¶(\d)
$1$2$3$4
(\d+)¶?
$1*_
_
This retina program replaces the input with the solution to the puzzle.
I have tested it on both the example and my own input. And despite being regex, it is really fast. It finishes without a single second on my machine.
How the math works
First, I searched for a fingerprint for each digit. A fingerprint must always have two properties:
- It must be unique for the object (in this case, digit)
- It must be invariant under changes that we do not know. (in this case, shuffling digits and segments
A fingerprint that does this can be found as follows:
Step 1: Take a specific segment. Count for all digits how many times it is 0.
For example, the top segment is on for the digits 0, 2, 3, 5, 6, 7, 8 and 9. So for that segment, we remember 8.

Doing this for the others yields 6, 8, 7, 4, 9, 7.






Step 2: Sum all the values of the segments which are on.
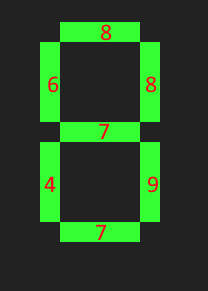
For example, for 0, almost all digits are on, so 8+6+8+4+9+7=42
We can do this for every number, giving:
1: 8+9=17
2: 8+8+7+4+7=34
3: 8+8+7+9+7=39
4: 6+8+7+9=30
5: 8+6+7+9+7=37
6: 8+6+7+4+9+7=41
7: 8+8+9=25
8: 8+6+8+7+4+9+7=49
9: 8+6+8+7+9+7=45
Efficient calculation
As our data is provided like this:
be cfbegad cbdgef fgaecd cgeb fdcge agebfd fecdb fabcd edb | fdgacbe cefdb cefbgd gcbe
We do not have to combine our segments into digits. We can calculate our fingerprint by counting the number of times each of the characters in our output digit appears on the pipe symbol’s left side.
Programming
Now that we have an algorithm, we can write a program as follows:
First, we create a separate line for each output digit:
([a-g ]+) \| ([a-g]+) ([a-g]+) ([a-g]+) ([a-g]+)
$1 | $2 ¶ $1 | $3 ¶ $1 | $4 ¶ $1 | $5
This will change be cfbegad cbdgef fgaecd cgeb fdcge agebfd fecdb fabcd edb | fdgacbe cefdb cefbgd gcbe to
be cfbegad cbdgef fgaecd cgeb fdcge agebfd fecdb fabcd edb | fdgacbe
be cfbegad cbdgef fgaecd cgeb fdcge agebfd fecdb fabcd edb | cefdb
be cfbegad cbdgef fgaecd cgeb fdcge agebfd fecdb fabcd edb | cefbgd
be cfbegad cbdgef fgaecd cgeb fdcge agebfd fecdb fabcd edb | gcbe
Then we open multiline mode with
%(`
Then for each line, we craft a new regex. Specifically, we make the first part of each statement a constant and the last part a list of characters.
([a-g ]+) \| ([a-g]+)
K`$1¶R`[$2]¶_
For example our first line
be cfbegad cbdgef fgaecd cgeb fdcge agebfd fecdb fabcd edb | fdgacbe
will be replaced by
K`be cfbegad cbdgef fgaecd cgeb fdcge agebfd fecdb fabcd edb
R`[fdgacbe]
_
This itself is a valid retina program
What is does is take whatever the left side of the system was a a constant.
And then replace every character that was on the right side by an underscore.
The next statement
~`$-
_
Will execute the retina program be build before as a retina program (so it is equivalent to an evalute). Notice that this is not injection proof. If we supply a tainted input data, we can execute arbitrary code.
This will replace our first line with
__ _______ ______ ______ ____ _____ ______ _____ _____ ___
__ ____ga_ ___g__ _ga___ _g__ ___g_ ag____ _____ _a___ ___
__ _____a_ ______ __a___ ____ _____ a_____ _____ _a___ ___
__ _f___ad __d__f f_a__d ____ fd___ a___fd f__d_ fa__d _d_
So every character that has to be counted is replaced by an underscore.
The next peiece of code replaces everything that isn’t an underscore with nothing. This removes everything except the underscores.
[^_]
So our first line becomes:
_________________________________________________
_______________________________________
_____________________________________________
______________________________
We then count the number of underscores in each line:
(_+)
$.1
So then each line is the correct fingerprint
49
39
45
30
The next two lines just close multi-line mode.
%)`
Then we apply the mapping from our fingerprints to our digits as stated in line one:
42
0
17
1
34
2
39
3
30
4
37
5
41
6
25
7
49
8
45
9
Each two lines is just a replace, so it read
key
value
key
value
...
Applying this changes our example into
8
3
9
4
The next piece of code:
(\d)¶(\d)¶(\d)¶(\d)
$1$2$3$4
Concatines each 4 lines back into a single number
So we replace our 4 digits with one number
8394
The next three lines sum all numbers
(\d+)¶?
$1*_
_
In essence, it replaces each number with that number of underscores, and then counts the number of underscores. This is a defaulkt way to sum things in unary.
So after doing everything we get the correct answer.