Advent of code 2021 day 8, seven segment displays, regex only solution.

I made a video about a specific technique to solve this puzzle using fingerprinting a while ago.

This technique is more efficient and faster than most methods I have seen online, but I still wondered if better, faster or fancier ways were possible.

So instead of building an actually fancier program, I created this:

([a-g ]+) \| ([a-g]+) ([a-g]+) ([a-g]+) ([a-g]+)
$1 | $2 ¶ $1 | $3 ¶ $1 | $4 ¶ $1 | $5
%(`([a-g ]+) \| ([a-g]+)
K`$1¶R`[$2]¶_
~`$-
_
[^_]

(_+)
$.1
%)`

42
0
17
1
34
2
39
3
30
4
37
5
41
6
25
7
49
8
45
9
(\d)¶(\d)¶(\d)¶(\d)
$1$2$3$4
(\d+)¶?
$1*_
_

Try it online

This retina program replaces the input with the solution to the puzzle.

I have tested it on both the example and my own input. And despite being regex, it is really fast. It finishes without a single second on my machine.

How the math works

First, I searched for a fingerprint for each digit. A fingerprint must always have two properties:

1. It must be unique for the object (in this case, digit)
2. It must be invariant under changes that we do not know. (in this case, shuffling digits and segments

A fingerprint that does this can be found as follows:

Step 1: Take a specific segment. Count for all digits how many times it is 0.

For example, the top segment is on for the digits 0, 2, 3, 5, 6, 7, 8 and 9. So for that segment, we remember 8.

Doing this for the others yields 6, 8, 7, 4, 9, 7.

Step 2: Sum all the values of the segments which are on.

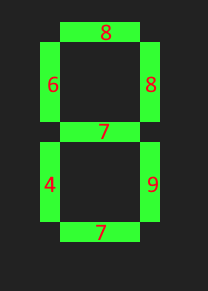
For example, for 0, almost all digits are on, so 8+6+8+4+9+7=42

We can do this for every number, giving:

1: 8+9=17

2: 8+8+7+4+7=34

3: 8+8+7+9+7=39

4: 6+8+7+9=30

5: 8+6+7+9+7=37

6: 8+6+7+4+9+7=41

7: 8+8+9=25

8: 8+6+8+7+4+9+7=49

9: 8+6+8+7+9+7=45

Efficient calculation

As our data is provided like this:

be cfbegad cbdgef fgaecd cgeb fdcge agebfd fecdb fabcd edb | fdgacbe cefdb cefbgd gcbe

We do not have to combine our segments into digits. We can calculate our fingerprint by counting the number of times each of the characters in our output digit appears on the pipe symbol’s left side.

Programming

Now that we have an algorithm, we can write a program as follows:
First, we create a separate line for each output digit:

([a-g ]+) \| ([a-g]+) ([a-g]+) ([a-g]+) ([a-g]+)
$1 | $2 ¶ $1 | $3 ¶ $1 | $4 ¶ $1 | $5

This will change be cfbegad cbdgef fgaecd cgeb fdcge agebfd fecdb fabcd edb | fdgacbe cefdb cefbgd gcbe to

be cfbegad cbdgef fgaecd cgeb fdcge agebfd fecdb fabcd edb | fdgacbe
be cfbegad cbdgef fgaecd cgeb fdcge agebfd fecdb fabcd edb | cefdb 
be cfbegad cbdgef fgaecd cgeb fdcge agebfd fecdb fabcd edb | cefbgd 
be cfbegad cbdgef fgaecd cgeb fdcge agebfd fecdb fabcd edb | gcbe

Then we open multiline mode with

%(`

Then for each line, we craft a new regex. Specifically, we make the first part of each statement a constant and the last part a list of characters.

([a-g ]+) \| ([a-g]+)
K`$1¶R`[$2]¶_

For example our first line

be cfbegad cbdgef fgaecd cgeb fdcge agebfd fecdb fabcd edb | fdgacbe

will be replaced by

K`be cfbegad cbdgef fgaecd cgeb fdcge agebfd fecdb fabcd edb 
R`[fdgacbe]
_

This itself is a valid retina program
What is does is take whatever the left side of the system was a a constant.
And then replace every character that was on the right side by an underscore.
The next statement

~`$-
_

Will execute the retina program be build before as a retina program (so it is equivalent to an evalute). Notice that this is not injection proof. If we supply a tainted input data, we can execute arbitrary code.

This will replace our first line with

__ _______ ______ ______ ____ _____ ______ _____ _____ ___
__ ____ga_ ___g__ _ga___ _g__ ___g_ ag____ _____ _a___ ___ 
__ _____a_ ______ __a___ ____ _____ a_____ _____ _a___ ___ 
__ _f___ad __d__f f_a__d ____ fd___ a___fd f__d_ fa__d _d_

So every character that has to be counted is replaced by an underscore.
The next peiece of code replaces everything that isn’t an underscore with nothing. This removes everything except the underscores.

[^_]

So our first line becomes:

_________________________________________________
_______________________________________ 
_____________________________________________ 
______________________________

We then count the number of underscores in each line:

(_+)
$.1

So then each line is the correct fingerprint

49
39
45
30

The next two lines just close multi-line mode.

%)`

Then we apply the mapping from our fingerprints to our digits as stated in line one:

42
0
17
1
34
2
39
3
30
4
37
5
41
6
25
7
49
8
45
9

Each two lines is just a replace, so it read

key 
value 
key 
value 
...

Applying this changes our example into

8
3
9
4

The next piece of code:

(\d)¶(\d)¶(\d)¶(\d)
$1$2$3$4

Concatines each 4 lines back into a single number
So we replace our 4 digits with one number

8394

The next three lines sum all numbers

(\d+)¶?
$1*_
_

In essence, it replaces each number with that number of underscores, and then counts the number of underscores. This is a defaulkt way to sum things in unary.

So after doing everything we get the correct answer.

Corona tests vs symptoms

Who is more likely to have covid? Someone who has a negative selftest,
but has cold-like symptoms, or someone with a positive test but who
has no symptoms?

Define the following:

C: patient has convid
T: patient tested positive
S: patient is symptomatic

We use the following data from the following sources

$P(S|\bar C) = 1/200$
from: https://www.cdc.gov/mmwr/volumes/70/wr/mm7029a1.htm and https://www.sciencedaily.com/releases/2012/06/120619225719.htm
combined to get symtpomatic common cold cases.
$P(S |C) = 1/2$
from https://edition.cnn.com/2020/04/01/europe/iceland-testing-coronavirus-intl/index.html
$P(C) = 367 639/11 000 000$
from https://www.worldometers.info/coronavirus/country/belgium/
$P(T|C) = 0.97$
$P(\bar T|\bar C) = 0.85$
https://covid-19.sciensano.be/nl/procedures/snelle-antigeen-ag-testen-0
And lets assume that the accuracy of the test is independent of the fact of the patient has symptomes
The last to givens can be extrapolated to
$P(\bar T|C) = 0.03$
$P(T|\bar C) = 0.15$
$P(\bar S|\bar C) = 0.995$
$P(\bar S |C) = 0.5$
$P(C) = 0.0334$
$P(\bar C) = 0.9665$

Law of bayes says:
$P(A \land B) = P(A|B)P(B)$

If A and B are independant under constant X that
$\begin{aligned}P(X|A \land B) &= P(X \land A \land B)/P(A \land B) \\ & = P(A \land B|X)P(X)/P(A \land B) \\ &= P(A|X)P(B|X)P(X)/P(A \land B) \\ &= P(A\land X)P(B \land X)/P(A \land B)P(X)\\ &= P(A\land X)P(B \land X)/(P(A \land B \land X) + P(A \land B \land \bar X))P(X) \\ &= P(A\land X)P(B \land X)/(P(A \land B|X)P(X) +P(A \land B|\bar X)P(\bar X))P(\bar X) \\ &= P(A\land X)P(B \land X)/(P(A|X)P(B|X)P(X) +P(A|\bar X)P(B|\bar X)P(\bar X))P(X) \\ &= P(A|X)P(B|X)P(X)/(P(A|X)P(B|X)P(X) +P(A|\bar X)P(B|\bar X)P(\bar X))\\ &= \frac{1}{1 + \frac{P(A|\bar X)P(B|\bar X)P(\bar X)}{P(A|X)P(B|X)P(X)}}\\ \end{aligned}$

$o(X|A \land B) = \frac{P(A|\bar X)P(B|\bar X)P(\bar X)}{P(A|X)P(B|X)P(X)}$

This gives

$\begin{aligned}P(C| \bar S \land T) &= \frac{1}{1 + \frac{P(\bar S|\bar C)P(T|\bar C)P(\bar C)}{P(\bar S|C)P(T|C)P(C)}}\\ \end{aligned}$

Filling in the given numbers this has a chance of 10,09%

And
$\begin{aligned}P(C|S \land \bar T) &= \frac{1}{1 + \frac{P(S|\bar C)P(\bar T|\bar C)P(\bar C)}{P(S|C)P(\bar T|C)P(C)}}\\ \end{aligned}$

Filling in the given numbers this has a chance of 10,87%

So having symptoms while having a negative test gives you the same chance to have covid as not having symptoms and having a positive test.

Magic 7 finite state machine

Consider the riddle in the following video

You can solve it as follows: You can write any number as $$x = \overline{x_nx_{n-1}...x_1x_0}$$ With the overline meaning concatenation, and $x_i$, the different digits of $x$. This notation is a shorthand for $$x = \sum 10^i x_i$$ We can rewrite this sum using distributivity to be $$ x = x_0 + 10(x_1 + 10(x_2 + ... )))$$ If we define our instuction $f_{x_i}$ as $$f_{x_i}(a) = x_i + 10a$$ Then $x$ can be written as $$ x = f_{x_0}(f_{x_1}(f_{x_2}( ... ))) $$ or $$ x = f_{x_0} \circ f_{x_1} \circ ... \circ f_{x_{n-1}}(x_n) $$ But as $f_{x_n}(0) = x_n$, it is more natural to write it as $$ x = f_{x_0} \circ f_{x_1} \circ ... \circ f_{x_{n-1}}\odot f_{x_n}(0) $$ We are only interested in whether or final result is a multiple of 7, ans as we only use multiplication and addition, we can consider the the full system in mod 7. $$ x \equiv f_{x_0} \circ f_{x_1} \circ ... \circ f_{x_{n-1}}\circ f_{x_n}(0) (\mod 7)$$ This formula now represents a finite state machine with 7 states, (0,1,2,3,4,5 and 6) and 10 instructions ($f_0$ to $f_9$), where the final state is the same a s the remainder of the original number when dividing by 7.

	0	1	2	3	4	5	6
0	0	3	6	2	5	1	4
1	1	4	0	3	6	2	5
2	2	5	1	4	0	3	6
3	3	6	2	5	1	4	0
4	4	0	3	6	2	5	1
5	5	1	4	0	3	6	2
6	6	2	5	1	4	0	3
7	0	3	6	2	5	1	4
8	1	4	0	3	6	2	5
9	2	5	1	4	0	3	6

Now, if we call state 0 X, state 1 A, state 2 C, state 3 F, state 4 B, state 5 D and state 6 E, we arrive at the transition table given by the riddle. So by consequence, the transition table works as a division test by 7.

Salamander riddle

Riddle

On a particular island live a lot of salamanders with different colours. Each salamander is defined by its genetics, an ordered list of unordered pairs of so-called genes. These genetics have the following properties:

1. A child of two salamanders will, for each gene pair, select one random gene from each parent and form a new gene pair with the two selections. (Kind of like how it works in real biology if we ignore random mutations and crossing over).
2. Two salamanders with the same gene pairs (so they are exact clones of each other) will have the same colour.
3. Two full siblings (so salamanders with the same parents) have the same colour (totally not how it works in biology).

Note that not all gene combinations have to be viable, so not every gene combination has a corresponding salamander.

Prove that two salamanders with different colours cannot have viable offspring.

Solution

Assume a salamander $X$ has genes $(x_1, x'_1), (x_2, x'_2), ...$ and a salamander $Y$ has genes $(y_1, y'_1), (y_2, y'_2), ...$. And they have viable offspring $Z$ with genes $(x_1, y_1), (x_2, y_2), ...$.
$X$ and $Z$ can have offspring genetically identical to $Z$ (by selecting $x_i$ from $X$ and $y_i$ from $Z$). And can have offspring that is genetically identical to $X$(by selecting $x'_i$ from $X$ and $x_i$ from $Z$). Therefore using the third axiom, $X$ and $Z$ have the same colour. Analogously, $Y$ and $Z$ have the same colour. By consequence, $X$ and $Y$ have to be the same colour.
You can find a more rigorous version of this proof that is a computer verified here: https://gitlab.com/Elmosfire/blog-links/-/blob/378a210994d4e5d5f96af505ebf1011aecbfca3f/salamander.lean.

Alternate version

If we soften the third axiom to be

Two full siblings have the same colour if neither of them is genetically equal to their parents.
In this case, a salamander can breed with another salamander of a different colour and produce viable offspring.
Assume there are three gene pairs, all with two possible genes. Call them r/R, g/G and b/B.
Then have only six viable gene combinations,
rRGGbb, rRggBB which are red.
rrgGBB, RRgGbb which are green,
RRggbB, rrGGbB which are blue.
And let each time call the first mentioned geneset to have left chirality and the right mentioned geneset to have right chirality.

Note that genesets of the same chirality are symmetric to one another by replacing r with g, g with b and b with r. Genes from the left chirality transform into genes with right chirality by swapping two genes.

Now we can check all cases:

• If a salamander breeds with a clone of itself, the only viable offspring is itself. For example, if rRGGbb breeds with itself, the offspring can only be RRGGbb, rRGGbb and rrGGbb, of which only the middle one is viable.
• If a salamander breeds with a salamander with the same chirality, it has one viable offspring. For example rRGGbb and rrgGBB only have rrGGbB as viable offspring.
• Two salamanders with the same colours but different chirality cannot have viable offspring.
• If two salamanders with different colours and chirality have offspring, the offspring always is a clone of one of the parents.
  If this argument does not convince you, you can check the system case by case:

rRGGbb(  red) & rRGGbb(  red) => <rRGGbb(  red)>
rRGGbb(  red) & rrgGBB(green) =>  rrGGbB( blue) 
rRGGbb(  red) & RRggbB( blue) =>  RRgGbb(green) 
rRGGbb(  red) & rRggBB(  red) => 
rRGGbb(  red) & RRgGbb(green) => <rRGGbb(  red)> or <RRgGbb(green)>
rRGGbb(  red) & rrGGbB( blue) => <rrGGbB( blue)> or <rRGGbb(  red)>
rrgGBB(green) & rRGGbb(  red) =>  rrGGbB( blue) 
rrgGBB(green) & rrgGBB(green) => <rrgGBB(green)>
rrgGBB(green) & RRggbB( blue) =>  rRggBB(  red) 
rrgGBB(green) & rRggBB(  red) => <rrgGBB(green)> or <rRggBB(  red)>
rrgGBB(green) & RRgGbb(green) => 
rrgGBB(green) & rrGGbB( blue) => <rrgGBB(green)> or <rrGGbB( blue)>
RRggbB( blue) & rRGGbb(  red) =>  RRgGbb(green) 
RRggbB( blue) & rrgGBB(green) =>  rRggBB(  red) 
RRggbB( blue) & RRggbB( blue) => <RRggbB( blue)>
RRggbB( blue) & rRggBB(  red) => <RRggbB( blue)> or <rRggBB(  red)>
RRggbB( blue) & RRgGbb(green) => <RRggbB( blue)> or <RRgGbb(green)>
RRggbB( blue) & rrGGbB( blue) => 
rRggBB(  red) & rRGGbb(  red) => 
rRggBB(  red) & rrgGBB(green) => <rrgGBB(green)> or <rRggBB(  red)>
rRggBB(  red) & RRggbB( blue) => <RRggbB( blue)> or <rRggBB(  red)>
rRggBB(  red) & rRggBB(  red) => <rRggBB(  red)>
rRggBB(  red) & RRgGbb(green) =>  RRggbB( blue) 
rRggBB(  red) & rrGGbB( blue) =>  rrgGBB(green) 
RRgGbb(green) & rRGGbb(  red) => <rRGGbb(  red)> or <RRgGbb(green)>
RRgGbb(green) & rrgGBB(green) => 
RRgGbb(green) & RRggbB( blue) => <RRggbB( blue)> or <RRgGbb(green)>
RRgGbb(green) & rRggBB(  red) =>  RRggbB( blue) 
RRgGbb(green) & RRgGbb(green) => <RRgGbb(green)>
RRgGbb(green) & rrGGbB( blue) =>  rRGGbb(  red) 
rrGGbB( blue) & rRGGbb(  red) => <rrGGbB( blue)> or <rRGGbb(  red)>
rrGGbB( blue) & rrgGBB(green) => <rrgGBB(green)> or <rrGGbB( blue)>
rrGGbB( blue) & RRggbB( blue) => 
rrGGbB( blue) & rRggBB(  red) =>  rrgGBB(green) 
rrGGbB( blue) & RRgGbb(green) =>  rRGGbb(  red) 
rrGGbB( blue) & rrGGbB( blue) => <rrGGbB( blue)>

If the salamander is in <>-brackets, it means it is a clone of one of the parents. You can quickly check two full siblings where none are a clone of either of the parents do not exist.
So the last hypothesis is fulfilled automatically.